Nguồn bài báo từ vnexpress:
https://vnexpress.net/dap-an-bai-toan-bon-quan-ma-tung-lam-kho-chu-nhan-giai-fields-4491210.html

Đề bài:

Hình dưới là chân dung Giáo sư June Huh cùng bài toán 4 quân mã đặt trên một phần của bàn cờ vua với ký hiệu W (Mã Trắng), B (Mã Đen) và các ô được đánh số từ 1 đến 10 trợ giúp bạn đọc ghi sơ đồ các bước đi.

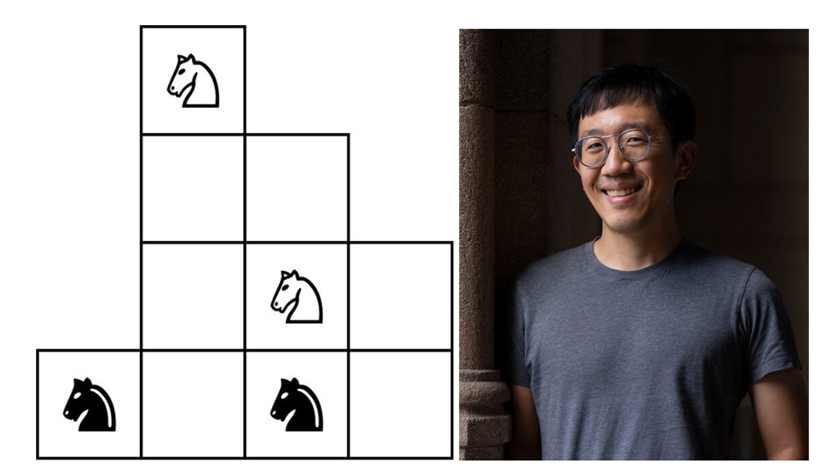
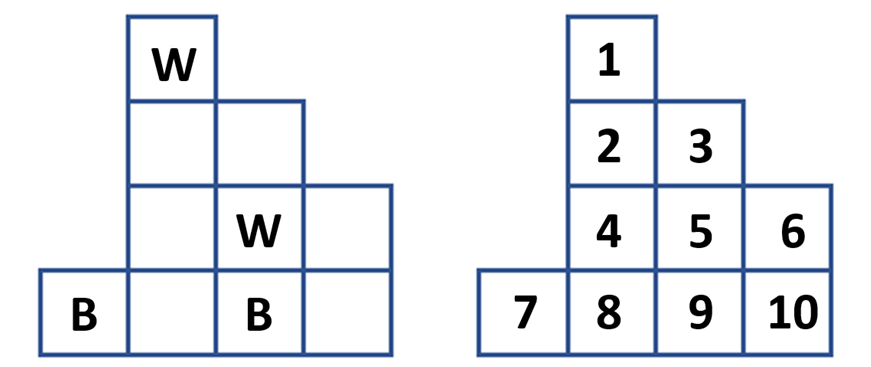
Hình dưới là chân dung Giáo sư June Huh cùng bài toán 4 quân mã đặt trên một phần của bàn cờ vua với ký hiệu W (Mã Trắng), B (Mã Đen) và các ô được đánh số từ 1 đến 10 trợ giúp bạn đọc ghi sơ đồ các bước đi.

1. Hãy xét xem có thể thực hiện 35 bước dịch chuyển để đổi chỗ vị trí 2 quân Mã Đen với 2 quân Mã Trắng cho nhau được hay không?

2. Sau ít nhất bao nhiêu bước dịch chuyển có thể đổi chỗ vị trí 2 quân Mã Đen với 2 quân Mã Trắng cho nhau?

Lời giải:

Đáp án: Cần ít nhất 40 bước dịch chuyển.

Bình luận của tác giả bài báo:

Cái hay của bài toán này là khi diễn đạt nó dưới dạng đồ thị, ta sẽ thấy ngay lời giải toán theo kiểu tiểu học: "tạo sơ đồ cho 4 quân mã đi liên tục như 4 tàu hỏa mà không nhảy cóc".

Việc tách ra 2 câu hỏi với gợi ý "câu một 35 bước" là để bạn đọc tiếp cận bài toán với một ước lượng gần đúng, tạo tâm lý tự tin không hoang mang "mò kim đáy bể" rồi thấm sâu triết lý: "giải một bài toán thú vị thường là đi từ cái sai đến cái gần đúng rồi mới đến cái đúng".

Đây cũng là quá trình mà Giáo sư June Huh đã trải nghiệm và ông gần như bỏ cuộc sau hàng trăm lần thử. Sau đó, ông nhận ra tấm bảng có hình dạng kỳ lạ và chuyển động hình chữ L của quân mã không phải là bản chất toán học. Điều quan trọng nhất chính là mối quan hệ giữa các ô vuông. Việc đúc kết lại một vấn đề thành một mô hình dễ hiểu hơn thường là chìa khóa để các nhà toán học tạo ra đột phá.